Atmospheric plasma: Where are the molecular bands of O₂?

When you take a spectrum of a discharge ignited in ambient air, it usually looks like this:

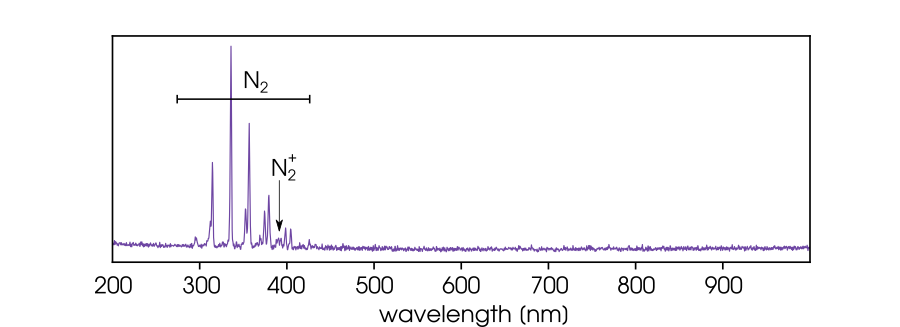
That’s no surprise, right? Plasma emission provides information about the gas composition. We have ignited the discharge in air, so we expect to see the emission of the air constituents.

So where on earth are the O₂ molecular bands?!

To answer this question, we need to take a look at the electronic states of molecular oxygen. The ground state is a triplet-Sigma-gerade-minus ( \(X\,^3\Sigma_g^-\) ). The first excited electronic state is singlet-Delta (\(a\,^1\Delta_g\)). The singlet-triplet transitions are extremely slow (unless you apply strong external fields), so the O₂ molecule, once excited to the singlet-Delta state, remains excited quite some time. It can eventually radiate at the near-infrared wavelengths around 1270 nm. But most likely, the energy will be carried by the molecule wherever it goes and will induce some interesting plasma kinetics there. That’s why singlet-Delta oxygen production is quite a topic – you can find nearly 600 papers with the words „singlet oxygen“ included in their titles!

When we look further up in the hierarchy of O₂ electronic states, we find the B-triplet-Sigma-ungerade-minus (\(B\,^3\Sigma_u^-\)) state. This one has everything to make a fine transition directly to the ground state: it’s a triplet, the orbital angular momenta align in the same manner (hence the \(\Sigma\)) and the ungerade-gerade transitions are strongly favored. That’s why this transition got an official name – the Schumann-Runge system.

The emission spectra of diatomic molecules consist of vibrational bands. Looking at the transition probabilities of the O₂ (B→X) transition, we expect the strongest O₂ emission for the bands with v’=0 and v“ from 9 to 16. These bands are located between 275 and 370 nm.

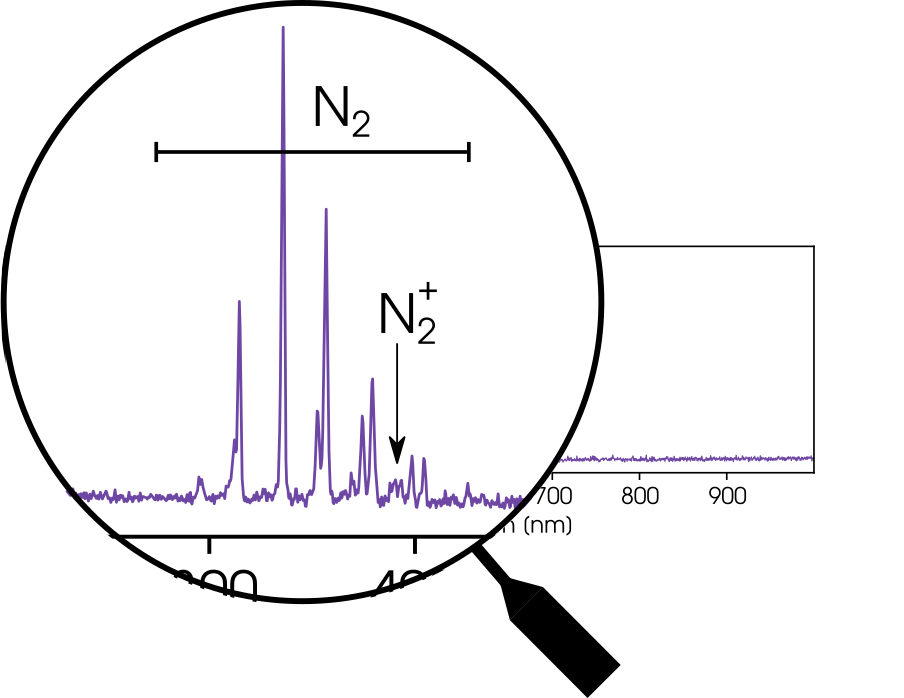
Nope. Just nitrogen. Why?

Let’s look at the potential energy diagram.

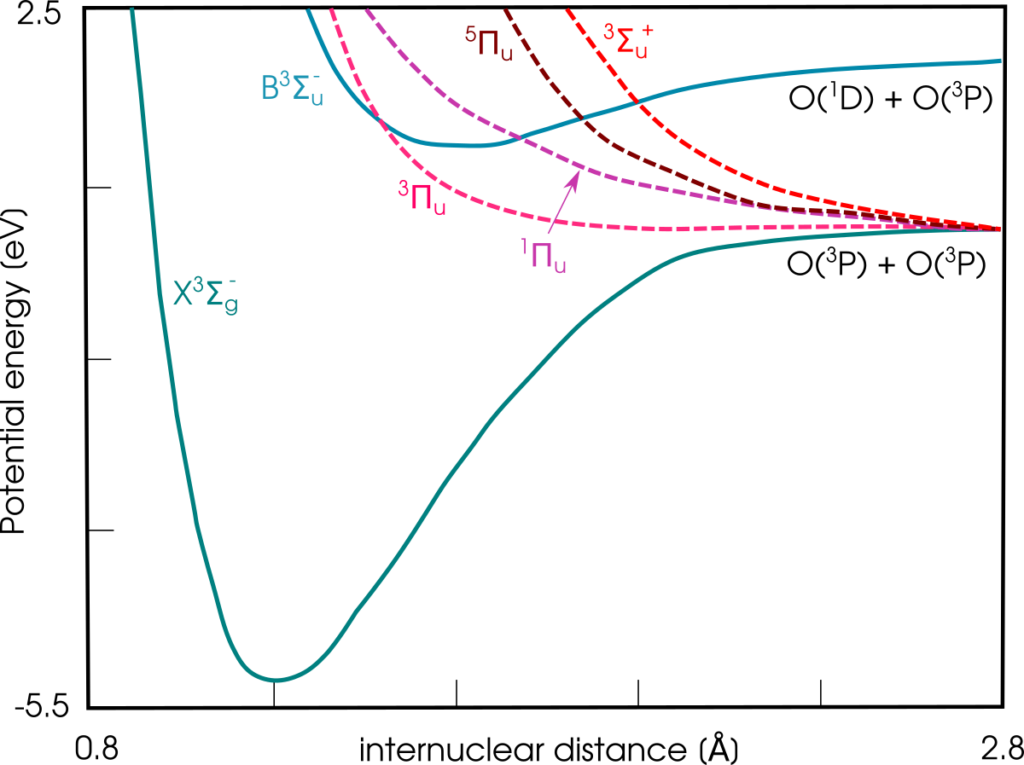
And there it is: the whole potential curve of the B-triplet-Sigma state lies above the dissociation limit. Moreover, there are 4 repulsive electronic states crossing with the B ³Σ. When the oxygen molecule has the opportunity to change the electronic state without overcoming any energetic barrier, sooner or later it chooses to do so. And then, there is no coming back, the result is two oxygen atoms in the ground triplet P states. This event is referred to as predissociation.

Cosby and others have measured the broadening of O₂ rotational lines to estimate the lifetimes τ of O₂(B) (which is a neat application of the quantum uncertainty principle), the result was around 50 ps. In other words, it takes only 50 picoseconds until 63% of the O₂(B) molecules either dissociate (with rate P, see below), radiate (with rate A), or give the energy away in a collision (with rate Q). The relation between the lifetime τ and the rates is simply

τ = 1 / (A+P+Q)

The Einstein emission coefficient of the most intense band starting at O₂(B, v’=0) is A = 2.8·10⁶ /s. We can now easily estimate the ratio of the number of O₂(B) molecules that radiate a photon due to the Schumann-Runge transition to the number of those that end up dissociated to two O atoms. We shall call this ratio the quantum yield of the spontaneous emission.

quantum yield = A / (A+P+Q) = A·τ = 1.4·10⁻⁴ = 1/7143

That is, only one O₂(B) molecule out of 7000 survives long enough to emit a photon!

Even though the Schumann-Runge bands are practically invisible in the emission, they can be readily found in absorption. For O₂(X, v=0) molecules, the absorption bands appear below 200 nm. This wavelength region is called vacuum ultraviolet (VUV) because the atmospheric oxygen absorbs the radiation, and you need to evacuate the beam path to avoid significant losses of the signal.

Now we know that VUV radiation is also an efficient tool for O₂ dissociation – once you excite the O₂(B) state, only 1 molecule in ~7000 relaxes back to the ground state, the other 7142 molecules dissociate. The free O atoms then attack everything around them, including the other O₂ molecules, eventually forming ozone. The human nose is a very sensitive ozone detector, so you can literally smell VUV light.

And that’s it!

Next time you’ll measure a spectrum of an atmospheric discharge, you won’t be surprised that you don’t see any bands of oxygen molecules. The first excited electronic state \( {\rm O}_2 (a\,^1\Delta_g) \) has different resulting electronic spin and therefore radiates extremely slowly. The next excited state, \( {\rm O}_2 (B\,^3\Sigma_u^-) \), lies entirely above the first dissociation limit and strongly prefers dissociation over radiation.